Hydrogen Molecular Ions
Although solid H2 has a low density compared to other solid materials, its density is enormous when compared with that of interstellar gas. Consequently chemical reactions taking place in the solid may follow different pathways to those occurring in molecular gas. A good example of this is the ionisation chemistry: when an energetic particle causes ionisation in molecular gas the end result is almost always the molecular ion H3+, whereas in solid H2 the molecular ion H6+ is favoured. Energetic particles are common in interstellar space, so we expect ionisation to occur and any particle of solid H2 will contain trace amounts of H6+. Thus one way of searching for hydrogen snowflakes is to look for signatures of H6+.
The propensity for ionisation events to yield H6+ in solid H2 was discovered only in the last decade, via electron spin resonance studies of irradiated solid H2 in the laboratory. To date there have been no laboratory studies of the electronic, vibrational or rotational transitions of this molecule, which is a pity because those are the transitions we're able to search for in the interstellar medium. Fortunately it's possible to calculate some of those properties using quantum theory, because these molecular ions contain only a small number of electrons.
The vibrational properties of H6+ and its isotopic variants, notably (HD)3+, were modelled by Leaf Lin and Andrew Gilbert (Research School of Chemistry, Australian National University), working in collaboration with Manly Astrophysics. Not all of the vibrational modes could be properly characterised, but those which could showed striking coincidences with known bands of mid-infrared emission or absorption in the interstellar medium, suggesting that molecular hydrogen ions could be responsible for the observed bands. The two figures below illustrate these coincidences.
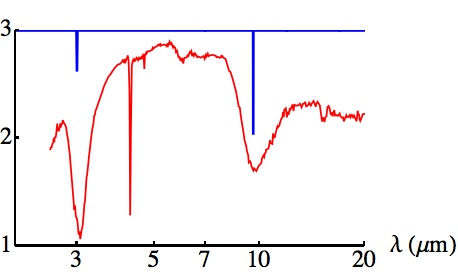The mid-infrared spectrum of the protostar Elias 29, plotted in red (taken from A.C.A. Boogert et al. Astronomy & Astrophysics, vol. 360, page 683). Also plotted, in blue, are the locations of the known lines of the H6+ molecule. The rotational band structure has not been modelled, so the blue lines show only the band centres, but note the coincidence with the two strongest absorption lines of Elias 29.
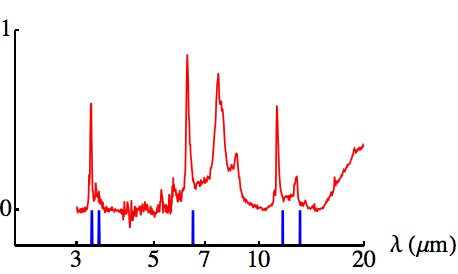The mid-infrared spectrum of the Orion Bar (a region in the Orion Nebula), plotted in red (taken from E. Peeters et al. 2004 in "Astrophysics of Dust", Astronomical Society of the Pacific Conference Series). Also plotted, in blue, are the locations of the known lines of the (HD)3+ molecule. The rotational band structure has not been modelled, so the blue lines show only the band centres, but note the coincidence with five of the strongest emission lines of the Orion Bar.
Leaf and Andrew's theoretical modelling was based on an analysis of the so-called "normal modes" of vibration. These modes, for both H6+ and (HD)3+, are shown in the animations below. Of these, the modes numbered 12, 11, 10, 7 and 6 are all good approximations to the true modes of vibration ("eigenmodes") of these molecular ions, whereas the other normal modes are not.
The difficulty of characterising the remaining eigenmodes stems from the fact that vibration mode #1 is actually more of an internal rotation than a vibration, as shown in the animation below.
Counter-rotation of the two end-units of H6+ causes variations in the energy associated with normal modes #2, 3, 4, 5, 8, 9, which tells us that these normal modes cannot be the true vibrational modes of the ion. These particular normal modes are problematic because they all involve movement of the central pair of atoms away from the long axis of the molecule, causing them to interact with the end units as they spin around. Further quantum chemical modelling, or laboratory spectroscopy of H6+ and (HD)3+ is needed to pin down the properties of these six vibrational eigenmodes.